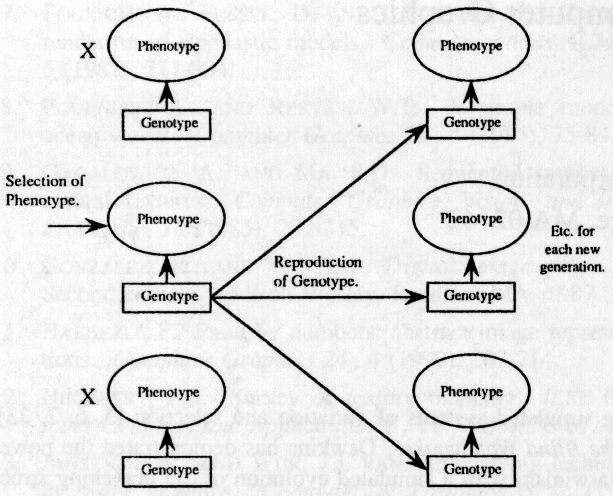
Figure 1: Phenotype selection, genotype reproduction.
Karl Sims
Thinking Machines Corporation
This paper describes how evolutionary techniques of variation and selection can be used to create complex simulated structures, textures, and motions for use in computer graphics and animation. Interactive selection, based on visual perception of procedurally generated results, allows the user to direct simulated evolutions in preferred directions. Several examples using these methods have been implemented and are described. 3D plant structures are grown using fixed sets of genetic parameters. Images, solid textures, and animations are created using mutating symbolic lisp expressions. Genotypes consisting of symbolic expressions are presented as an attempt to surpass the limitations of fixed-length genotypes with predefined expression rules. It is proposed that artificial evolution has potential as a powerful tool for achieving flexible complexity with a minimum of user input and knowledge of details.
Procedural models are increasingly employed in computer graphics to create scenes and animations having high degrees of complexity. A price paid for this complexity is that the user often loses the ability to maintain sufficient control over the results. Procedural models can also have limitations because the details of the procedure must be conceived, understood, and designed by a human. The techniques presented here contribute towards solutions to these problems by enabling ``evolution'' of procedural models using interactive ``perceptual selection.'' Although they do not give complete control over every detail of the results, they do permit the creation of a large variety of complex entities which are still user directed, and the user is not required to understand the underlying creation process involved.
Many years ago Charles Darwin proposed the theory that all species came about via the process of evolution [2]. Evolution is now considered not only powerful enough to bring about biological entities as complex as humans and consciousness, but also useful in simulation to create algorithms and structures of higher levels of complexity than could easily be built by design. Genetic algorithms have shown to be a useful method of searching large spaces using simulated systems of variation and selection [23][7][6][5]. In The Blind Watchmaker, Dawkins has demonstrated the power of Darwinism with a simulated evolution of 2D branching structures made from sets of genetic parameters. The user selects the ``biomorphs'' that survive and reproduce to create each new generation [4][3]. Latham and Todd have applied these concepts to help generate computer sculptures made with constructive solid geometry techniques [28][9].
Variations on these techniques are used here with the emphasis on the potential of creating forms, textures, and motions that are useful in the production of computer graphics and animation, and also on the potential of using representations that are not bounded by a fixed space of possible results.
Both biological and simulated evolutions involve the basic concepts of genotype and phenotype, and the processes of expression, selection, and reproduction with variation.
The genotype is the genetic information that codes for the creation of an individual. In biological systems, genotypes are normally composed of DNA. In simulated evolutions there are many possible representations of genotypes, such as strings of binary digits, sets of procedural parameters, or symbolic expressions. The phenotype is the individual itself, or the form that results from the developmental rules and the genotype. Expression is the process by which the phenotype is generated from the genotype. For example, expression can be a biological developmental process that reads and executes the information from DNA strands, or a set of procedural rules that utilize a set of genetic parameters to create a simulated structure. Usually, there is a significant amplification of information between the genotype and phenotype.
Selection is the process by which the fitness of phenotypes is determined. The likelihood of survival and the number of new offspring an individual generates is proportional to its fitness measure. Fitness is simply the ability of an organism to survive and reproduce. In simulation, it can be calculated by an explicitly defined fitness evaluation function, or it can be provided by a human observer as it is in this work.
Reproduction is the process by which new genotypes are generated from an existing genotype or genotypes. For evolution to progress there must be variation or mutations in new genotypes with some frequency. Mutations are usually probabilistic as opposed to deterministic. Note that selection is, in general, non-random and is performed on phenotypes; variation is usually random and is performed on the corresponding genotypes [See figure 1].

Figure 1: Phenotype selection, genotype reproduction.
The repeated cycle of reproduction with variation and selection of the most fit individuals drives the evolution of a population towards higher and higher levels of fitness.
Sexual combination can allow genetic material of more than one parent to be mixed together in some way to create new genotypes. This permits features to evolve independently and later be combined into a single individual. Although it is not necessary for evolution to occur, it is a valuable practice that can enhance progress in both biological and simulated evolutions.
Genetic algorithms were first developed by Holland [11] as robust searching techniques in which populations of test points are evolved by random variation and selection. They have become widely used in a number of applications to find optima in very large search spaces [23][7][6].
Genetic algorithms differ from the examples presented in this paper in that they usually utilize an explicit analytic function to measure the fitness of phenotypes. Since it is difficult to automatically measure the aesthetic visual success of simulated objects or images, here the fitness is provided by a human user based on visual perception. Some combinations of automatic selection and interactive selection are also utilized.
Population sizes used for genetic algorithms are usually fairly large (100 to 1000 or more) to allow searching of many test points and avoiding only local optima. At each generation, many individuals survive and reproduce to create the next generation. For the examples presented in this paper, the success of a solution is dependent on human opinion, therefore there is no single global optimum. Many local optima are potentially interesting solutions. For this reason, and also because of user interface practicality, a smaller population size has been used (20 - 40), and only one or two individuals are chosen to reproduce for each new generation.
Genotypes used in genetic algorithms traditionally consist of fixed-length character strings used by fixed expression rules. This is appropriate for searching predefined dimensional spaces for optimum solutions, but these restrictions are sometimes limiting. Koza [13][12] has used hierarchical lisp expressions as genotypes such that the dimensionality of the search space itself can be extended to successfully solve problems such as artificial ant navigation and game strategies. Discovery systems, such as AM, Eurisko, and Cyrano, also utilize a form of mutating lisp programs [14][8]. The examples of evolving images, volume textures, and animations presented here also use genotypic representations composed of lisp expressions, although the set of functions used includes various vector transformations, noise generators, and image processing operations, as well as standard numerical functions.
In the next section, techniques for using artificial evolution to explore samples in parameter spaces are discussed. In section 4, examples of evolving images, volume textures, and animations which utilize mutating symbolic expressions as genotypes are presented. Finally, results, suggestions for future work, and conclusions are given in the last three sections.
Procedural models such as fractals, graftals, and procedural texturing allow a user to create a high degree of complexity with relatively simple input information [25][21][19][18]. One method of procedural structure creation involves a set of N input parameters each of which has an effect on a developmental process which assembles the structure. The set of possible structures corresponds to the N-dimensional space of possible parameter values. Consider an array of knobs, each controlling one parameter, that can be experimentally turned to adjust the results. As more options are added to the procedure for more variation of results, the number of input parameters grows and it can become increasingly difficult for a user to predict the effects of adjusting particular parameters and combinations of parameters, and to adjust the knobs effectively by hand.
An alternative approach is to sample randomly in the neighborhood of a currently existing parameter set by making random alterations to a parameter or several parameters, then inspect and select the best sample or samples of those presented. This allows exploration through the parameter space in incremental arbitrary directions without requiring knowledge of the specific effects of each parameter. This is artificial evolution in which the genotype is the parameter set, and the phenotype is the resulting structure. Selection is performed by the user picking preferred phenotypes from groups of samples, and as long as the samples can be generated and displayed quickly enough, it can be a useful technique.
The first example of artificial evolution involves 3D plant structures which can be grown using a set of ``genetic'' parameters. Plant generation algorithms of various types have been shown to be useful examples of procedurally generated structures [29][25][22][21][16][1]. The model used in this work is described briefly below, but details have been omitted as the emphasis is on the evolutionary process.
Parameters describing fractal limits, branching factors, scaling, stochastic contributions, etc., are used to generate 3-dimensional tree structures consisting of connected segments. Growth rules use 21 genetic parameters and the hierarchy location of each segment in the tree to determine how fast that segment should grow, when it should generate new buds, and in which directions. The tree structures are grown in arbitrarily small increments for smooth simulation of development.
After a desirable tree structure has been evolved using interactive selection and the mutation methods described below, its phenotype can be saved for further manipulation. Solid polygonal branches can be generated with connected cylinders and cone shapes, and leaves can be generated by connecting sets of peripheral nodes with polygonal surfaces. Shading parameters, color, and bump textures can be assigned to make bark and leaf surfaces. These additional properties could also be selected and adjusted using artificial evolution, but due to the longer computation times involved to test samples, these parameters were adjusted by hand. In some cases, leaf shapes were evolved independently and then explicitly added to the tip segments of other evolved plant structures. A forest of plant structures created using these methods is shown in figure 3.
For artificial evolution of parameter sets to occur, they must be reproduced with some probability of mutation. There are many possible methods for mutating parameter sets. The technique used here involves normalizing each parameter for a genetic value between .0 and 1.0, and then copying each genetic value or gene, gi, from the parent to the child with a certain probability of mutation, m. A mutation is achieved by adding a random amount, +-d, to the gene. So, a new genotype, G', is created using each gene, gi, of a parent genotype, G, as follows:
For each gi If rand(.0,1.0) < m then g'i = gi + rand(-d, d) clamp or wrap g'i to legal bounds. else g'i = gi
The normalized values are scaled, offset, and optionally squared to give the parameter values actually used. This allows the mutation distances, +-d, to be proportional to the scale of the range of valid parameter values. Squaring or raising some values to even higher powers can be useful because it causes more sensitivity in the lower region of the range of parameter values. The mutation rate and amount are easily adjusted, but are commonly useful at much higher values than in natural systems (m=0.2, d=0.4). The random value between -d and d might preferably be found using a Gaussian distribution instead of this simple linear distribution, giving smaller mutations more likelihood than larger ones.
When two parameter sets are found that both create structures with different successful features, it is sometimes desirable to combine these features into a single structure. This can be accomplished by mating them. Reproducing two parameter sets with sexual combination can be performed in many ways. Four possible methods are listed below with some of their resulting effects:
Mutating and mating parameter sets allow a user to explore and combine samples in a given parameter space. In the next section, methods are presented that allow mutations to add new parameters and extend the space, instead of simply adjusting existing parameter values.

Figure 2: Mating plant structures.

Figure 3: Forest of ``evolved'' plants.
A limitation of genotypes consisting of a fixed number of parameters and fixed expression rules as described above is that there are solid boundaries on the set of possible phenotypes. There is no possibility for the evolution of a new developmental rule or a new parameter. There is no way for the genetic space to be extended beyond its original definition - the N-dimensional genetic space will remain only N-dimensional.
To surpass this limitation, it is desirable to include procedural information in the genotype instead of just parameter data, and the procedural and data elements of the genotype should not be restricted to a specific structure or size.
Symbolic lisp expressions are used as genotypes in an attempt to meet these needs. A set of lisp functions and a set of argument generators are used to create arbitrary expressions which can be mutated, evolved, and evaluated to generate phenotypes. Some mutations can create larger expressions with new parameters and extend the space of possible phenotypes, while others just adjust existing parts of the expression. Details of this process are best described by the examples below.
The second example of artificial evolution involves the generation of textures by mutating symbolic expressions. Equations that calculate a color for each pixel coordinate (x,y) are evolved using a function set containing some standard common lisp functions [26], vector transformations, procedural noise generators, and image processing operations:
+, -, *, /, mod, round, min, max, abs, expt, log, and,
or, xor, sin, cos, atan, if, dissolve, hsv-to-rgb, vector,
transform-vector, bw-noise, color-noise, warped-bw-noise,
warped-color-noise, blur, band-pass, grad-mag, grad-dir,
bump, ifs, warped-ifs, warp-abs, warp-rel, warp-by-grad.
Each function takes a specified number of arguments and calculates and returns an image of scalar (b/w) or vector (color) values.
Noise generators can create solid 2D scalar and vector noise at various frequencies with random seeds passed as arguments so specific patterns can be preserved between generations [figure 4f, and 4i]. The warped versions of functions take (U,V) coordinates as arguments instead of using global (X,Y) pixel coordinates, allowing the result to be distorted by an arbitrary inverse mapping function [figure 4i]. Boolean operations (and, or, and xor) operate on each bit of floating-point numbers and can cause fractal-like grid patterns [figure 4e]. Versions of sin and cos which normalize their results between .0 and 1.0 instead of -1.0 and 1.0 can be useful. Some functions such as blurs, convolutions, and those that use gradients also use neighboring pixel values to calculate their result [figure 4h]. Band-pass convolutions can be performed using a difference of Gaussians filter which can enhance edges. Iterative function systems (ifs) can generate fractal patterns and shapes.

Figure 4: Simple expression examples.
(reading left to right, top to bottom) a. X b. Y c. (abs X) d. (mod X (abs Y)) e. (and X Y) f. (bw-noise .2 2) g. (color-noise .1 2) h. (grad-direction (bw-noise .15 2) .0 .0) i. (warped-color-noise (* X .2) Y .1 2)
Details of the specific implementations of these functions are not given here because they are not as important as the methods used for combining them into longer expressions. Many other functions would be interesting to include in this function set, but these have provided for a fairly wide variety of resulting images.
Simple random expressions are generated by choosing a function at random from the function set above, and then generating as many random arguments as that function requires. Arguments to these functions can be either scalars or vectors, and either constant values or images of values. Random arguments can be generated from the following forms:
- A random scalar value such as .4
- A random 3-element vector such as #(.42 .23 .69)
- A variable such as the X or Y pixel coordinates.
- Another lisp expression which returns a b/w or color image.
Most of the functions have been adapted to either coerce the arguments into the required types, or perform differently according to the argument types given to them. Arguments to certain functions can optionally be restricted to some subset of the available types. For the most part these functions receive and return images, and can be considered as image processing operations. Expressions are simply evaluated to produce images. Figure 4 shows examples of some simple expressions and their resulting images.
Artificial evolution of these expressions is performed by first generating and displaying a population of simple random expressions in a grid for interactive selection. The expressions of images selected by the user are reproduced with mutations for each new generation such that more and more complex expressions and more perceptually successful images can evolve. Some images evolved with this process are shown in figures 9 to 13.
Symbolic expressions must be reproduced with mutations for evolution of them to occur. There are several properties of symbolic expression mutation that are desirable. Expressions should often be only slightly modified, but sometimes significantly adjusted in structure and size. Large random changes in genotype usually result in large jumps in phenotype which are less likely to be improvements, but are necessary for extending the expression to more complex forms.
A recursive mutation scheme is used to mutate expressions. Lisp expressions are traversed as tree structures and each node is in turn subject to possible mutations. Each type of mutation occurs at different frequencies depending on the type of node:
Other types of mutations could certainly be implemented, but these are sufficient for a reasonable balance of slight modifications and potential for changes in complexity.
It is preferable to adjust the mutation frequencies such that a decrease in complexity is slightly more probable than an increase. This prevents the expressions from drifting towards large and slow forms without necessarily improving the results. They should still easily evolve towards larger sizes, but a larger size should be due to selection of improvements instead of random mutations with no effect.
The relative frequencies for each type of mutation above can be adjusted and experimented with. The overall mutation frequency is scaled inversely in proportion to the length of the parent expression. This decreases the probability of mutation at each node when the parent expression is large so that some stability of the phenotypes is maintained.
The evaluation of expressions and display of the resulting images can require significant calculation times as expressions increase in complexity. To keep image evolution at interactive speeds, estimates of compute speeds are calculated for each expression by summing pre-computed runtime averages for each function. Slow expressions are eliminated before ever being displayed to the user. New offspring with random mutations are generated and tested until fast enough expressions result. In this way automatic selection is combined with interactive selection. If necessary, this technique could also be performed to keep memory usage to a minimum.
Symbolic expressions can be reproduced with sexual combinations to allow sub-expressions from separately evolved individuals to be mixed into a single individual. Two methods for mating symbolic expressions are described.
The first method requires the two parents to be somewhat similar in structure. The nodes in the expression trees of both parents are simultaneously traversed and copied to make the new expression. When a difference is encountered between the parents, one of the two versions is copied with equal probability. For example, the following two parents can be mated to generate four different expressions, two of which are equal to the parents, and two of which have some portions from each parent:
parent1: (* (abs X) (mod X Y)) parent2: (* (/ Y X) (* X -.7))child1: (* (abs X) (mod X Y)) child2: (* (abs X) (* X -.7)) child3: (* (/ Y X) (mod X Y)) child4: (* (/ Y X) (* X -.7))
This method is often useful for combining similar expressions that each have some desired property. It usually generates offspring without very large variations from the parents. Two expressions with different root nodes will not form any new combinations. This might be compared to the inability of two different species to mate and create viable offspring.
The second method for mating expressions combines the parents in a less constrained way. A node in the expression tree of one parent is chosen at random and replaced by a node chosen at random from the other parent. This crossing over technique allows any part of the structure of one parent to be inserted into any part of the other parent and permits parts of even dissimilar expressions to be combined. With this method, the parent expressions above can generate 61 different child expressions - many more than the 4 of the first method.
A third variable, Z, is added to the list of available arguments to enable functions to be evolved that calculate colors for each point in (X,Y,Z) space. The function set shown in section 4.1 is adjusted for better results: 2D functions that require neighboring pixel values such as convolutions and warps are removed, and 3D solid noise generating functions are added.
These expressions are more difficult to visualize because they encompass all of 3D space. They are evaluated on the surfaces of spheres and planes for fast previewing and selection as shown in figure 5. Evolved volume expressions can then be incorporated into procedural shading functions to texture arbitrary objects. This process allows complex volume textures such as those described in [18] and [19] to be evolved without requiring specific equations to be understood and carefully adjusted by hand. Figure 6 was generated by evolving three volume texture expressions and then evaluating them at the surfaces positions of three objects during the rendering process.

Figure 5: Parent with 19 random mutations.

Figure 6: Marble and wooden tori.
Several extensions to the image evolution system described above can be used to evolve moving images. Five methods for incorporating a temporal dimension in symbolic expressions are proposed:

Figure 7: Frames from a ``genetic cross dissolve.''

Figure 8: Fire of Faces.
Finally, the techniques above can be used together in various combinations to make an even wider range of possibilities for evolving animations.
Evolution of 3D plant structures, images, solid textures, and animations have been implemented on the Connection Machine (R) system CM-2, a data parallel supercomputer [27][10]. The parallel implementation details will not be discussed in this paper, but each application is reasonably suited for highly parallel representation and computation. Lisp expression mutations and combinations are performed on a front-end computer and the Connection Machine system is used to evaluate the expression for all pixels in parallel using Starlisp and display the resulting image.
3D Plant structures have been evolved and used in the animated short Panspermia [24]. A frame from this sequence is shown in figure 3 which contains a variety of species created using these techniques. An interactive system for quickly growing, displaying, and selecting sample structures allows a wide range of plant shapes to be efficiently created by artificial evolution. Populations of samples can be displayed for selection in wire frame in a grid format as shown in figure 2, or displayed as separate higher-resolution images which can be interactively flipped through by scrolling with a mouse. Typically between 5 and 20 generations are necessary for acceptable structures to emerge.
Images, volume textures, and various animations have been created using mutating symbolic expressions. These sometimes require more generations to evolve complex expressions that give interesting images - often at least 10 to 40 generations. Again, an interactive tool for quickly displaying grids of sample images to be selected amongst makes the evolution process reasonably efficient. [See figure 5.] The number of possible symbolic expressions of acceptable length is extremely large, and a wide variety of textures and patterns can occur. Completely unexpected kinds of images have emerged. Figure 9 was created from the following evolved expression:
(round (log (+ y (color-grad (round (+ (abs (round
(log (+ y (color-grad (round (+ y (log (invert y) 15.5))
x) 3.1 1.86 #(0.95 0.7 0.59) 1.35)) 0.19) x)) (log (invert
y) 15.5)) x) 3.1 1.9 #(0.95 0.7 0.35) 1.35)) 0.19) x)

Figure 9

Figure 10

Figure 11
Figure 13 was created from this expression:
(sin (+ (- (grad-direction (blur (if (hsv-to-rgb (warped-
color-noise #(0.57 0.73 0.92) (/ 1.85 (warped-color-
noise x y 0.02 3.08)) 0.11 2.4)) #(0.54 0.73 0.59) #(1.06
0.82 0.06)) 3.1) 1.46 5.9) (hsv-to-rgb (warped-color-
noise y (/ 4.5 (warped-color-noise y (/ x y) 2.4 2.4))
0.02 2.4))) x))
Note that expressions only five or six lines long can generate images of fair complexity. Equations such as these can be evolved from scratch in timescales of only several minutes - probably much faster than they could be designed.
Figures 10, 11, and 12 were also created from expressions of similar lengths. Fortunately, analysis of expressions is not required when using these methods to create them. Users usually stop attempting to understand why each expression generates each image. However, for those interested, expressions for other figures are listed in the appendix.
Two different approaches of user selection behavior are possible. The user can have a goal in mind and select samples that are closer to that goal until it is hopefully reached. Alternatively, the user can follow the more interesting samples as they occur without attempting to reach any specific goal.
The results of these various types of evolved expressions can be saved in the very concise form of the final genotypic expression itself. This facilitates keeping large libraries of evolved forms which can then be used to contribute to further evolutions by mating them with other forms or further evolving them in new directions.

Figure 12

Figure 13
Artificial evolution has many other possible applications for computer graphics and animation. Procedures that use various other forms of solid noise could be explored, such as those that create objects, create density functions, or warp objects [15][20]. Procedures could be evolved that generate motion from a set of rules (possibly cellular automata, or particle systems), or that control distributions and characteristics of 2D objects such as lines, solid shapes, or brush strokes. Algorithms that use procedural construction rules to create 3D objects from polygons, or functions that generate, manipulate, and combine geometric primitives could also be explored.
These techniques might also make valuable tools in domains beyond computer simulations. New possibilities for shapes and textures could be explored for use in product design or the fashion industry.
Several variations on the methods for artificial evolution described above might make interesting experiments. Mutation frequencies could be included in the genotype itself so that they also can be mutated. This might allow for the evolution of evolvability [4]. Frequencies from the most successful evolutions could be kept as the defaults.
It might be interesting to attempt to automatically evolve a symbolic expression that could generate a simple specific goal image. An image differencing function could be used to calculate a fitness based on how close a test image was to the goal, and an expression could be searched for by automatic selection. Then, interactive selection could be used to evolve further images starting with that expression.
Large amounts of information of all the human selection choices of many evolutions could be saved and analyzed. A difficult challenge would be to create a system that could generalize and ``understand'' what makes an image visually successful, and even generate other images that meet these learned criteria.
Combinations of random variations and non-random variations using learned information might be helpful. If a user picks phenotypes in a certain direction from the parent, mutations for the next generation might have a tendency to continue in that same direction, causing evolution to have ``momentum.''
Also, combinations of evolution and the ability to apply specific adjustments to the genotype might allow more user control over evolved results. Automatic ``genetic engineering'' could permit a user to request an evolved image to be more blue, or a texture more grainy.
Artificial evolution has been demonstrated to be a potentially powerful tool for the creation of procedurally generated structures, textures, and motions. Reproduction with random variations and survival of the visually interesting can lead to useful results. Representations for genotypes which are not limited to fixed spaces and can grow in complexity have shown to be worthwhile.
Evolution is a method for creating and exploring complexity that does not require human understanding of the specific process involved. This process of artificial evolution could be considered as a system for helping the user with creative explorations, or it might be considered as a system which attempts to ``learn'' about human aesthetics from the user. In either case, it allows the user and computer to interactively work together in a new way to produce results that neither could easily produce alone.
An important limiting factor in the usefulness of artificial evolution is that samples need to be generated quickly enough such that it is advantageous for the user to choose from random samples instead of carefully adjusting new samples by hand. The computer needs to generate and display samples fast enough to keep the user interested while selecting amongst them. As computation becomes more powerful and available, artificial evolution will hopefully become advantageous in more and more domains.
Thanks to Lew Tucker, Jim Salem, Gary Oberbrunner, Matt Fitzgibbon, Dave Sheppard, and Pattie Maes for help and support. Thanks to Peter Schröder for being a helpful and successful user of these tools. Thanks to Luis Ortiz and Katy Smith for help with document preparation. And thanks to Danny Hillis, Larry Yaeger, and Richard Dawkins for discussions and inspiration.
Figure 5, Parent expression:
(warped-color-noise (warped-bw-noise (dissolve x 2.53 y) z 0.09 12.0) (invert z) 0.05 -2.06)
Figure 6, Marble torus:
(dissolve (cos (and 0.25 #(0.43 0.73 0.74))) (log (+ (warped-bw-noise (min z 11.1) (log (rotate-vector (+ (warped-bw-noise (cos x) (dissolve (cos (and 0.25 #(0.43 0.73 0.74))) (log (+ (warped-bw-noise (max (min z 8.26) (/ -0.5 #(0.82 0.39 0.19))) (log (+ (warped-bw-noise (cos x) z -0.04 0.89) #(0.82 0.39 0.19)) #(0.15 0.34 0.50)) -0.04 -3.0) y) #(0.15 0.34 0.50)) y) -0.04 -3.0) x) z y) #(0.15 0.34 0.5)) -0.02 -1.79) -0.4) #(-0.09 0.34 0.55)) -0.7)
Figure 7, Cross dissolve:
(hsv-to-rgb (bump (hsv-to-rgb (ifs 2.29 0.003 (dissolve 1.77 3.67 time) 2.6 0.1 (dissolve 5.2 3.2 time) -31.0 (dissolve 23.9 -7.4 time) (dissolve 1.13 9.5 time) (dissolve 4.8 0.16 time) 20.7 4.05 (dissolve 0.48 0.46 time) (dissolve 2.94 -0.68 time) (dissolve 0.42 0.54 time) (dissolve 0.09 0.54 time))) (atan 2.25 (dissolve 0.1 0.11 time) 0.15) (dissolve 4.09 8.23 time) (dissolve #(0.41 0.36 0.08) #(0.68 0.22 0.31) time) #(0.36 0.31 0.91) (dissolve 6.2 4.3 time) (dissolve 0.16 0.40 time) (dissolve 2.08 0.23 time)))
Figure 8, Fire of Faces:
(+ (min 10.8 (warp-rel image image (bump image x 9.6 #(0.57 0.02 0.15) #(0.52 0.03 0.38) 3.21 2.49 10.8))) (dissolve #(0.81 0.4 0.16) x (dissolve y #(0.88 0.99 0.66) image)))
Figure 10:
(rotate-vector (log (+ y (color-grad (round (+ (abs (round (log #(0.01 0.67 0.86) 0.19) x)) (hsv-to-rgb (bump (if x 10.7 y) #(0.94 0.01 0.4) 0.78 #(0.18 0.28 0.58) #(0.4 0.92 0.58) 10.6 0.23 0.91))) x) 3.1 1.93 #(0.95 0.7 0.35) 3.03)) -0.03) x #(0.76 0.08 0.24))
Figure 11 is unfortunately ``extinct'' because it was created before the genome saving utility was complete.
Figure 12:
(cos (round (atan (log (invert y) (+ (bump (+ (round x y) y) #(0.46 0.82 0.65) 0.02 #(0.1 0.06 0.1) #(0.99 0.06 0.41) 1.47 8.7 3.7) (color-grad (round (+ y y) (log (invert x) (+ (invert y) (round (+ y x) (bump (warped-ifs (round y y) y 0.08 0.06 7.4 1.65 6.1 0.54 3.1 0.26 0.73 15.8 5.7 8.9 0.49 7.2 15.6 0.98) #(0.46 0.82 0.65) 0.02 #(0.1 0.06 0.1) #(0.99 0.06 0.41) 0.83 8.7 2.6))))) 3.1 6.8 #(0.95 0.7 0.59) 0.57))) #(0.17 0.08 0.75) 0.37) (vector y 0.09 (cos (round y y)))))