
Answer
Please respect these puzzles: be patient and think for awhile before you click on the answer!
Strange Trip
| You travel 100 miles north, 100 miles east, and then 100 miles south. You are at the same point that you started from. Describe all the places on earth this could be, if any. |
Hint Answer |
Three Cards
| There are 3 cards: one is all red, one is all blue, and the third is blue on one side and red on the other. The cards are shuffled. You pick one at random and it is blue on the side facing you. What are the chances it is also blue on the other side? |
Hint Answer |
Monty Hall Problem
| Behind 1 of 3 closed doors is a prize. You pick one of the doors. Monty, knowing where the prize is, opens one of the other doors which is empty. You are given the choice of sticking with your choice or switching to the other unopened door. Should you switch? What are your chances of winning if you do? Assume Monty always opens an empty door. |
Hint Answer |
4 Door Monty Hall Problem
| Behind 1 of 4 closed doors is a prize. You pick door 1. Monty, knowing where the prize is, opens the 4th door which is empty. You switch your choice to door 2. Now Monty opens another door which is empty: door 3. Given the choice, should you switch back to door 1, and what are your chances of winning if you do? Assume Monty always opens doors that are empty. | Answer |
Monty Fall Problem
| Behind 1 of 3 closed doors is a prize. You pick one of the doors. Monty accidentally slips and falls, knocking one of the other doors open at random which happens to be empty. You are given the choice of sticking with your choice or switching to the other unopened door. What are your chances of winning if you switch? |
Hint Answer |
Two Envelopes
| There are two envelopes, one contains twice as much money as the other. You pick one at random and find $100 inside. What is the "expected value" of the amount in the other envelope? Given the option, should you switch? Does it matter how much you found in that first envelope? Does it matter if you open the envelope? |
Hint Answer |
Three Envelopes
| There are three envelopes with different amounts of money in them. You pick one at random and open it. You then have the option to switch and open a second envelope. Again, you may switch to the third envelope if you'd like. However, if you switch you must discard the opened envelope and you can never switch back to it. Is there a strategy that gives you better than 1/3 chances of getting the best envelope, and if so what are those chances? |
Hint Answer |
What's Next?
What is the next figure in this sequence?

|
Hint Answer |
Helium
| A helium balloon is in your car. How does it move when you slam on the brakes? |
Hint Answer |
Urns with Balls
| There are 2 urns filled with 100 ping pong balls total. 50 ping pong balls are white and 50 are black. I reach randomly into one of the urns, stir, and pick one ball without looking. What are the highest possible chances of me picking a white one that you can cause if you arrange the balls in the urns ahead of time? |
Hint Answer |
Bean Bag
| A bag contains a single bean, known to be either white or black. A new white bean is added to the bag, and it is shaken. A bean is taken back out, and it is white. What are the chances the remaining bean is also white? |
Hint Answer |
Apples and Oranges
| Three boxes each contain 20 pieces of fruit and are labeled "apples", "oranges", and "apples and oranges". The labels were correct but have been mixed up and are now all on the wrong boxes. What is the minimum number of fruits you need to inspect to learn the correct contents of all three boxes? | Answer |
4 Boxes of Fruit
| Four unlabled boxes contain one type of fruit each: apples, oranges, pears, and bananas. Knowing this, 100 people guess which boxes contain which type of fruit. 30 people guess all 4 wrong, 40 guess only 1 fruit correctly, and 23 guess 2 of the fruits correctly. How many guess 3 correctly, and how many guess all 4 of them correctly? |
Hint Answer |
Four Trees
| A farmer claims to have 4 trees on his land all equidistant from each other. Could this be true? |
Hint Answer |
Suicidal Spots
| In a far away land, there is an unusual tribe of 300 perfectly logical and perfectly intelligent people. Each member has a visible spot on the back of his or her head, some are red and some are black. Nobody knows the color of their own spot, but they do know the color of everyone else's. If a tribesman ever realizes the color of his own spot it is strict custom that he publicly commit suicide the following morning, so they never mention spot colors, and have no mirrors. But then one day an American tourist visits this land and announces to the entire tribe: "I can see that at least one of you has a red spot." The tourist leaves and returns a year later. What has happened? |
Hint Answer |
One Question
|
You are shipwrecked on an island. There is a fork in the path to the
other side, one way leads to a safe village, the other leads to hungry
cannibals. There are twin brothers who both know which path is which,
but one of the brothers is honest, and the other always lies. You may
ask one of them a single question. What should it be?
Related puzzle: what one question would you ask if there is just one person who is honest or lies but you don't know which? | Answer |
Three Random Hats
| Three people are given hats. Each hat is either red or blue, chosen at random. Each person can see the other 2 hats, but not their own. They each must simultaneously either guess their own hat's color, or pass. No communication is allowed, although they can agree on a strategy ahead of time. What strategy will give them the best chances of at least one person guessing right, and nobody guessing wrong? |
Hint Answer |
Two Random Hats
| Two people are given hats. Each hat is either black or white, chosen at random. Each person can see the other hat, but not their own. They each must simultaneously guess their own hat's color. No communication is allowed, although they can agree on a strategy ahead of time. What strategy will give them the best chances of at least one person guessing right? (In this version there is no penalty for a wrong guess if the other guesses right.) |
Hint Answer |
String Around the Earth
| Imagine a long string tied tightly around the entire earth. One meter is then added to its total length. The slack is evenly distributed, and the string is somehow made to hover slightly above the ground at the same height all the way around the world. Ignore mountains and oceans, and assume the earth is perfectly round. What is the largest creature that could now fit under the string: ant, cricket, mouse, or cat? |
Hint Answer |
Northwest Spiral
| Two pilots fly from the Equator to the North Pole. The first flies north in a straight path. The second flies on a spiral path by always heading northwest. How far does the second pilot travel? (relative to the first) | Answer |
Odd Ball
| There are 12 equal sized balls. One ball has a slightly different weight (more or less) than the other 11. Can you use a balance scale only 3 times to find the odd ball? | Answer |
Six Balls
| You have 6 balls: 2 red, 2 white, and 2 blue. One of each color is slightly heavier, but the 3 heavy ones weigh the same, and the 3 light ones weigh the same. Can you use a balance scale only 2 times to find the 3 heavy balls? | Hint Answer |
Bags of Gold
| Ten bags each contain nine pieces of gold. The gold pieces are all supposed to weigh 1 ounce, but the pieces in one bag weigh only .9 ounces. Use an accurate scale just once to find which bag contains the lighter pieces. | Answer |
Fair Cake
| When two people want to share a cake fairly, one cuts, and the other chooses. Assuming this is a fair scheme, devise a similar scheme for 3 people and 1 cake. Nobody should get short caked even if the other 2 cooperate. | Answer |
Light Switches
| There are 3 incandescent light bulbs in one room and 3 switches for these bulbs in another room. No light from the bulbs can be seen outside of their room. You are allowed to enter the room with the bulbs only once. How can you figure out which switches are connected to which bulbs? | Answer |
Grid of Tiles
| There is an empty 8x8 grid, except two opposite corners are missing. Can you tile the rest with 1x2 tiles? | Answer |
1x3 Tiles
| Can you cover an 8x8 grid with 1x3 tiles and a single 1x1 tile? If so, in what locations can the 1x1 tile be? | Answer |
Cheese Cubes
| A block of cheese is cut into a 3x3x3 grid of sub-cubes. A mouse starts eating one corner, and moves on to adjacent pieces until they are all eaten. Could he eat the middle piece last? |
Hint Answer |
Measuring with Jugs
|
Using a 5 liter jug, a 3 liter jug, and a hose, can you measure 4
liters of water? How about measuring 1 liter? |
Hint Answer |
Burning Fuses
| You have 2 lengths of fuse and 2 matches. One fuse will burn from start to end in 10 minutes, and the other in 15 minutes. However, their burn rate is not steady along their lengths. Measure 20 minutes of time. |
Hint Answer |
Rope Escape
| You have 150 meters of rope and a knife and need to escape from the roof of a 200 meter burning building. There are places to tie the rope to the building only at the roof, and at a ledge halfway down. How can you make it down without jumping? | Answer |
Pocket Change
| If all the coins in my pocket except two are pennies, all except two are nickels, and all except two are dimes, how much money do I have? | Answer |
Gloves and Germs
| You have 3 cultures of highly contagious and deadly germs. As part of an important experiment you must squeeze each culture once with your entire hand. However, you have only 1 pair of latex gloves. You must not contaminate any culture with another or with germs from your skin. The gloves can be worn on either the left or right hand. How can you complete your experiment without contaminating anything? | Answer |
Mixed Up Liquids
| There are two equally filled jars, one contains milk, the other water. A teaspoon of milk goes into the water and is stirred. Then a teaspoon of the mixture goes back into the milk. Is there more water in the milk or milk in the water? | Answer |
Feynman's Sucking Sprinkler
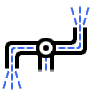
| If you take a water sprinkler like the one above and put it under water, it will spin clockwise as it would on land. But what happens if you then reverse the flow so it sucks in water? Would it spin, and if so, in which direction? | Answer |
Train Full of Water
| A train car is at rest on a frictionless track. The car is full of water and has a spout pointing downwards on the far right end. The spout is opened and the water pours out. Describe the movement of the car, if any. |
Hint Answer |
Superball Battle
| Joe and Billy are having a one-dimensional battle by shooting at each other through a long frictionless tube. Their guns each fire 10 balls in rapid succession, and all the balls enter the tube before any collide. The balls are perfectly elastic, have equal mass, are are shot at the same speed. Where do the balls end up and how many total bounces occur? | Answer |
Bubbles in Space
| Two balls of matter in empty space would move towards each other. What if all space were filled with a frictionless deformable substance, except for two empty bubbles? How would the bubbles move? | Answer |
Flipped Cards
| You are blindfolded and given a deck of 52 cards with 10 of the cards flipped upside down at random. Can you somehow arrange the deck into two piles that contain the same number of flipped cards? | Hint Answer |
Fox in a Hole
| There are 5 holes in a row. A fox spends each day in a hole, but always moves to an adjacent hole the next day, either right or left. You want to find the fox but you only get to inspect one hole per day. What is a strategy for finding the fox in the fewest days? |
Hint Answer |
Six Chop Sticks
| Using 6 equal length chop sticks make exactly 4 equilateral triangles. |
Hint Answer |
Stick Boxes
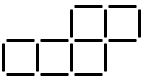
Make 4 equal sized squares out of these 5 by moving only 2 sticks, and leave no extra sticks. |
Hint Answer |
Fish Sticks

Point the fish the other way by moving only 3 sticks. | Answer |
Ten Points
| Can you arrange 10 points so that 5 lines can each be drawn through 4 points? | Answer |
Connect the Dots

Connect these 9 dots with only 4 connected straight line segments. (Don't lift your pencil.) | Answer |
Four Points and Two Distances
| Arrange 4 points in a plane so there are only 2 distinct distances between the 6 pairs of points. How many configurations like this are there? |
Hint Answer |
Six Marbles
| If you have 2 red, 2 green, and 2 blue marbles, can you arrange them so each one touches all four marbles of a different color? |
Hint Answer |
Wire Cube
| What is the minimum number of wires needed to make a cube? You can bend, but do not double, the wires. |
Hint Answer |
Cube Vision
| What is the maximum number of sides of a cube that you could see at once? The cube may be any size. The sides are opaque so you can't see through them, and you can't use mirrors or other reflections. |
Hint Answer |
Cube Sides
| You have 6 differently colored squares that fit together to make the sides of a cube. How many different kinds of cubes could you make with these? |
Hint Answer |
Five Triangles
Can you arrage five 1x2 right triangles to make a square? You may cut
only one of the triangles into two pieces. All of the triangle pieces must
be used to fill the square with no overlaps. You can rotate or flip
the triangles but they should remain flat.

|
Hint Answer |
30-60-90 Triangles
Can you cut a 30-60-90 triangle into 3 smaller but equal sized 30-60-90 triangles?
How about into 4 of them? How many ways are possible for each?

For a harder problem: how many ways to cut into 9 of them? | Answer |
Bookworm
| A encyclopedia with ten 200 page volumes is sitting on a bookshelf in the usual order. A bookworm starts at the first page and eats in a straight line to the last page. How many total pages does he eat through? | Answer |
Five Pirates
| Five pirates of different ages have 100 gold coins, and they decide to split the coins using the following rules: the oldest pirate proposes how to divide the coins, and all pirates vote for or against that plan. If 50% or more of the pirates approve, then the coins will be shared that way. Otherwise, the pirate proposing the plan is thrown overboard, and the process is repeated with the remaining pirates. Assume all the pirates are predictably very intelligent and very greedy. What will happen? |
Hint Answer |
100 Pirates
| Similar to above but with the quantities flipped: 100 pirates of different ages have 5 gold coins, and they decide to split the coins using the following rules: the oldest pirate proposes how to divide the coins, and all pirates vote for or against that plan. If 50% or more of the pirates approve, then the coins will be shared that way. Otherwise, the pirate proposing the plan is thrown overboard, and the process is repeated with the remaining pirates. Assume all the pirates are predictably very intelligent and very greedy. Also if a pirate figures his vote will not make a difference, he'll act in a bloodthirsty way and vote against the plan. What will happen? | Answer |
Five Hats
| Three wise men are lined up in single file, each wearing a white hat. They know there were 5 hats total, three white, and two black, but they can only see the hats on the men in front of them. They don't speak unless they figure out what color hat they have on. Who figures out first? | Answer |
Pop Quiz
| A teacher announces there will be a surprise quiz sometime during the week. The students argue it can't be on Friday because if the teacher waits until the last day it won't be a surprise anymore. Once they know it can't be Friday they argue by the same reasoning that it can't be Thursday either. What is wrong with this logic? | Answer |
Darts
| You throw two darts at a dart board, aiming for the center. The second lands farther from the center than the first. You then throw another dart at the board, aiming for the center. Assume your skill level is consistent. What are the chances that this third dart also lands farther from the center than the first? | Answer |
Girl Babies
| A large tribe obeys a strict reproductive custom. All families continue having children until they have a girl, and then they stop having more children. Assume it is equally likely for a given birth to produce a girl or boy, and assume families can have any number of children so they always do get one girl eventually. In the 10th generation, what is the expected ratio of males to females? Also, what is the expected population size of the 10th generation relative to the 1st? | Answer |
Hotel Bellboy
| Three people check into a hotel. They pay $30 to the manager and go to their room. The manager finds out that the room rate is $25 and gives $5 to the bellboy to return. On the way to the room the bellboy reasons that $5 would be difficult to share among three people so he pockets $2 and gives $1 to each person. Now each person paid $10 and got back $1. So they paid $9 each, totaling $27. The bellboy has $2, totaling $29. Where is the remaining dollar? | Answer |
Doctor Who
| A father and his son are in a car crash. The father is killed instantly but the son is only injured and is taken to the hospital. He is rushed to the operating room, the doctor comes in, looks at the patient on the operating table, and says, "I can't operate on him, he's my son." How can this be? | Answer |
Two Fathers and Two Sons
| Two fathers and two sons are in a boat. One person falls overboard, but there are only two people left in the boat. How can this be? | Answer |
Two Boys and a Boat
| Two boys wish to cross a river. The only way to the other side is by boat, but the boat can only take one boy at a time. The boat can not return on its own and there are no ropes or similar tricks, yet both boys manage to cross using the boat. How? |
Hint Answer |
4 People and a Bridge
| A family of four must quickly cross a precarious bridge over a dangerous river at night. They have only one torch and need it for every crossing. No more than two people can be on the bridge at the same time or it will break and they will fall to their deaths. Each person is able to walk at a different speed: they take at least 1 minute, 2 minutes, 7 minutes, and 10 minutes to cross respectively. What is the fastest they can all get safely across? |
Hint Answer |
Defying Death
| A thief is caught and sentenced to death, but the king allows him to make one last statement which will also determine his method of execution. He is to be hanged if his statement is true, or he is to be fed to lions if his statement is false. Somehow he manages to live. What did he say? | Answer |
Non-Self Containing Sets
| What is difficult about the set of all sets that do not contain themselves? | Answer |
Manhole Covers
| Why are manhole covers round? | Answer |
Mirrors
| Why do mirrors seem to flip things left-right but not up-down? | Answer |
Mind Reading Trick
| Pick a random integer between 1 and 10. Put a zero on the end to make it ten times larger, then subtract your original number from that. Sum the digits of this new number, and subtract 4. Then turn this number into a letter: 1 becomes A, 2 becomes B, 3 becomes C, 4 becomes D, etc. Now think of a land animal who's name begins with that letter. It can be large or small, mammal, reptile, or amphibian, but can not fly or swim. Select the first one that comes to your mind. See if you picked as predicted... and why does this work? | Answer |
Centrifuge
| Can you spin 5 samples in a 12-hole centrifuge, without it being out of balance? | Answer |
1000 Doors
| A thousand doors start closed. Someone walks along and changes the state of each door (opens or closes). A 2nd person changes the state of every 2nd door, and a 3rd person changes the state of every 3rd door. This continues until the 1000th person changes the state of the 1000th door. How can you know if the Nth door is now open or closed? (without simulating the whole thing) | Answer |
Three Dice
| You roll three dice, and multiply the resulting numbers together. What are the chances that product is odd? | Answer |
Two Dice at 7
| If you roll two dice, what are the chances they add to 7? (This is a warm-up for the next problem.) | Answer |
Four Dice at 14
| If you roll four dice, what are the chances they add to 14? | Answer |
Meet in the Middle
| You are negotiating to buy a Persian rug where they often overcharge tourists. You offer 1/2 the asking price, and the salesman says he can meet you in the middle at 3/4. You then offer to meet him in the middle again (between 1/2 and 3/4) and he does the same back to you again (between 5/8 and 3/4). What price would you arrive at if you continued like this forever? | Answer |
Alien Hats
| You are among 10 humans abducted by aliens who will be given an intelligence test to determine if earth is worth saving. You will be lined up single file and each given a white or black hat, at random. Nobody will see the color of their own hat, nor can they see the hats on the people behind them, but they can see the hats on all the people in front of them. Then, one at a time, each person must guess the color of their own hat, starting with the person in the back who sees all the others, and ending with the person in the front who sees nothing. No other communication is allowed except the single guess "black" or "white" from each person. No delays or tone of voice signals are allowed. If anybody except the first person guesses wrong, everyone is killed and earth is destroyed. Fortunately you have some time before the test to discuss and agree on a strategy. Can you save the planet, and if so how? | Hint Answer |
100 Prisoners and 100 Boxes
| A room has 100 boxes labeled 1 to 100, containing the names of 100 prisoners, one name per box in a random order. These 100 prisoners visit the room one by one, and each is allowed to inspect up to 50 boxes, one after the other. If all the prisoners somehow each manage to find their own name in a box, they are all released. The prisoners may not change anything in the room or communicate any information to the others after entering the room. However they are allowed to meet ahead of time and devise a plan. Is there a strategy that allows all of the prisoners to find their names with some reasonable probability? |
Hint Answer |
Wire Ends
| A new undersea cable is laid connecting a remote island to the mainland. The cable contains 36 wires, however the cable company neglected to label or color-code the wire ends to indicate which wires are which. You have one battery and one light bulb for testing, and plenty of labels to tag each wire on both ends, so they can be properly attached to the equipment the following day. However, there is nobody to help you, and there is only time to travel once from the mainland to the island and back. Is there a strategy that allows you to identify and label the matching ends of all 36 wires in just one round trip? |
Hint Answer |
Ball Paths

| A ball is dropped into the top of the stack of boxes as shown. The boxes are open on the top and bottom so if there are 2 boxes below, the ball can fall either to the left or right. How many possible paths are there from the top to the bottom box? (The ball never bounces back up, and motion within a box doesn't matter. A path is a unique sequence of boxes that the ball passes through.) |
Hint Answer |
Ball Paths 2

| Similar to above, a ball is dropped into the top of the stack of boxes and falls down to the bottom box. For each level, when there are 2 boxes below, the ball falls randomly left or right with equal chances. (Assume the direction the ball came from the previous level does not affect the next bounce.) Two of the many possible paths from top to bottom are shown. Which of these paths is more likely, or are they equally likely? |
Hint Answer |
Square of Bugs
| Four bugs are on the corners of a 1 meter square. Each bug always faces the next bug (on the next clockwise corner). If they all walk forward at the same speed until they meet, how far does each bug travel? | Answer |
Bike Speed
| A biker rode a mile in 3 minutes with the wind, and returned in 5 minutes against the wind. How fast could he ride a mile with no wind? |
Hint Answer |
A Bee and Two Trains
| Two trains are 30 miles apart, and travel towards each other at 5 mph and 10 mph. A bee starts at the slower train and flies at 25 mph to the other train. Each time it reaches a train it turns around and flies back to the other train again. What is the sum of the distances that the bee has flown when the trains meet? |
Hint Answer |
Backwards Bee and Two Trains
| Two trains start end-to-end at the same point and travel away from each other at 5 mph and 10 mph. A bee also starts at the same point and flies back and forth at 25 mph between the ends of the moving trains. After 2 hours, where is the bee? |
Hint Answer |
Water Levels
| You are on a boat in a small pond. You have a stone and a log in the boat. You throw the stone into the water. Does the water level in the pond rise, fall or stay the same? How about if you throw the log in? |
Hint Answer |
Refueling
| You want to be the first to circumnavigate a newly discovered planet, but your surveillance spaceship can only hold enough fuel to fly half way around it, and there is only one spaceport where you can land. The spaceport has ample fuel, and there are two other spaceships available that can transfer fuel while flying, but their tanks are the same size, so also only hold enough fuel to fly half way around the planet. The ships always fly at the same speed, but assume the refueling times and the effects of fuel weight or changing directions are inconsequential. Can you devise a plan to fly your ship all the way around the planet without any ships running out of fuel and crashing before they return safely to port? |
Hint Answer |
Pieces of Stone
| A farmer has a 40 lb stone that he uses to measure out bales of hay on a 2 sided balance. He loans it to a friend who accidentally breaks it into 4 pieces. Instead of being angry, the farmer is quite happy. He says to the friend, "you managed to break it into just the right 4 pieces that will now let me weigh any weight between 1 and 40." What are the weights of the 4 pieces? |
Hint Answer |
Breaking Balls
| You have 2 bowling balls that each breaks when dropped from the same height. You want to find the highest floor of a 100 story building from which these balls can be dropped without breaking. Devise an optimal procedure that can always locate that floor using not more than N drop tests. What is the smallest N can be? |
Hint Answer |
Puzzling Scales
|
Here is a classic old puzzle from Samuel Loyd (1841-1911). Assume the
3 blocks weigh the same amount as each other, and the 12 marbles weigh
the same amount as each other. How many marbles will balance the top?
| Hint Answer |
Magic Microbes
|
Count the microbes in the picture below. There are 14.
Now swap the top two rectangular pieces of the image, and count them again.
A 15th microbe has appeared! Where does it come from? Print one of these images and cut along the black lines to make three rectangular pieces. Then you can physically swap the top two rectangles to show the trick. |
Hint Answer |
Handshakes
| Jack and his wife attend a party with 4 other couples. Each person shakes hands with those they don't already know. Jack then asks each person how many hands they shook, and to his surprise he gets 9 different answers. How many hands did Jack and his wife each shake? |
Hint Answer |
Three-Way Duel
| Joe, John, and Jack have an argument and agree to a 3-way dual. They will take turns shooting until only one man is left standing. Joe is given the first shot because he is the worst aim and can only hit his target 1/2 of the time. John goes second and is on-target 3/4 of the time. Jack always hits his target, and will shoot third if he is still standing for his turn. What is the best strategy for Joe's first shot, and who is most likely to win? |
Hint Answer |
Find the Cable
| You urgently need to find an underground fiber optic cable that will allow you to listen to enemy communication and save your fleet from destruction. You know this cable is buried 1 meter underground and passes somewhere straight through a 1x1 square kilometer of land that you control. What is the minimum total length of ditches you need to dig to be sure to find the cable? |
Hint Answer |
karlsims![]() gmail
gmail![]() com
com