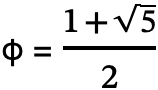Golden Ratio Tutorial
Karl Sims
The golden ratio, represented by the Greek letter phi, is the unique
positive value who's reciprocal is the same as subtracting 1, and square
is the same as adding 1.
φ ≈ 1.6180339887
1/φ ≈ 0.6180339887
φ2 ≈ 2.6180339887
Golden rectangles
A golden rectangle has a side ratio of φ. When a square is
added or subtracted from this rectangle, a new golden rectangle is
created with the same proportions, on its side.
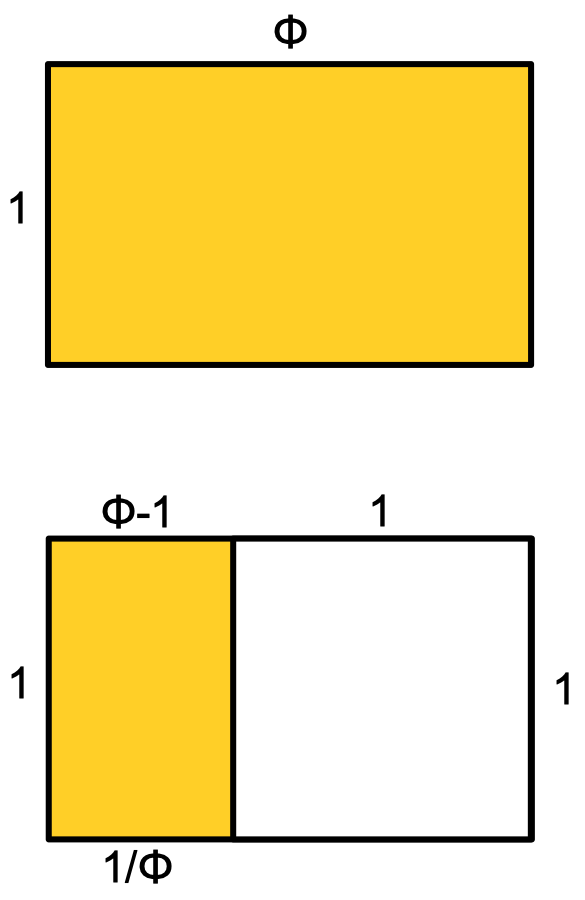
When a golden rectangle is divided into a rectangle and a
square, the new smaller rectangle has the same proportions, but turned
sideways. The height of the new rectangle is 1 and the width is
1/φ to give the same ratio. But its width is also φ - 1
because the square with sides 1 was removed from the original width of
φ. So this works if 1/φ = φ - 1.
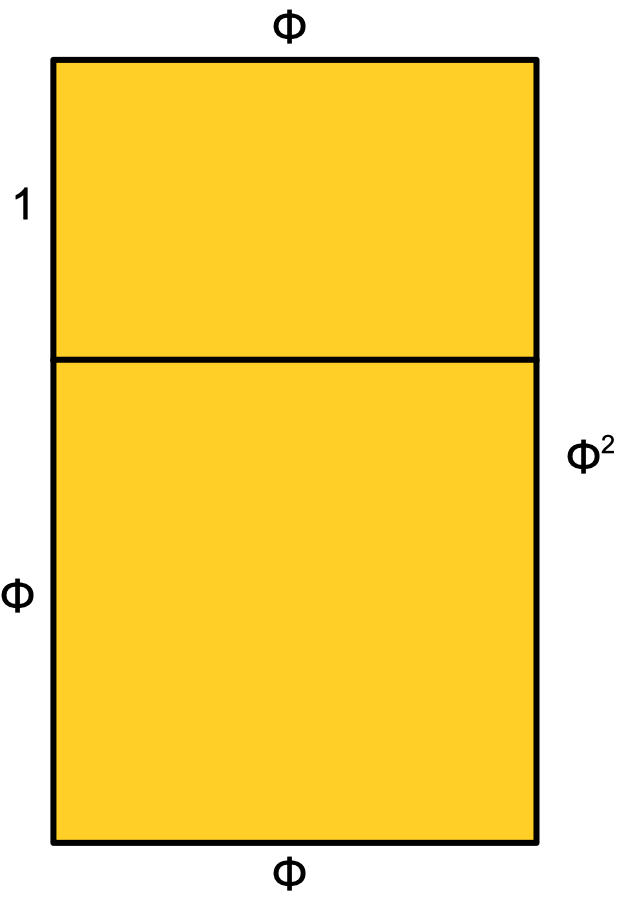
Similarly when a larger φ x φ square is added below the golden
rectangle, the resulting larger rectangle also has the same
proportions. The width of the new rectangle is φ and the height
is φ2 to give the same ratio. But its height is also
φ + 1 because the square with sides φ was added to the
original height of 1. So this works if φ2 = φ + 1.
The value of φ can be calculated from either of these identities.
Using the quadratic formula to find the positive root of
φ2 - φ - 1 = 0, gives:
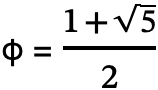
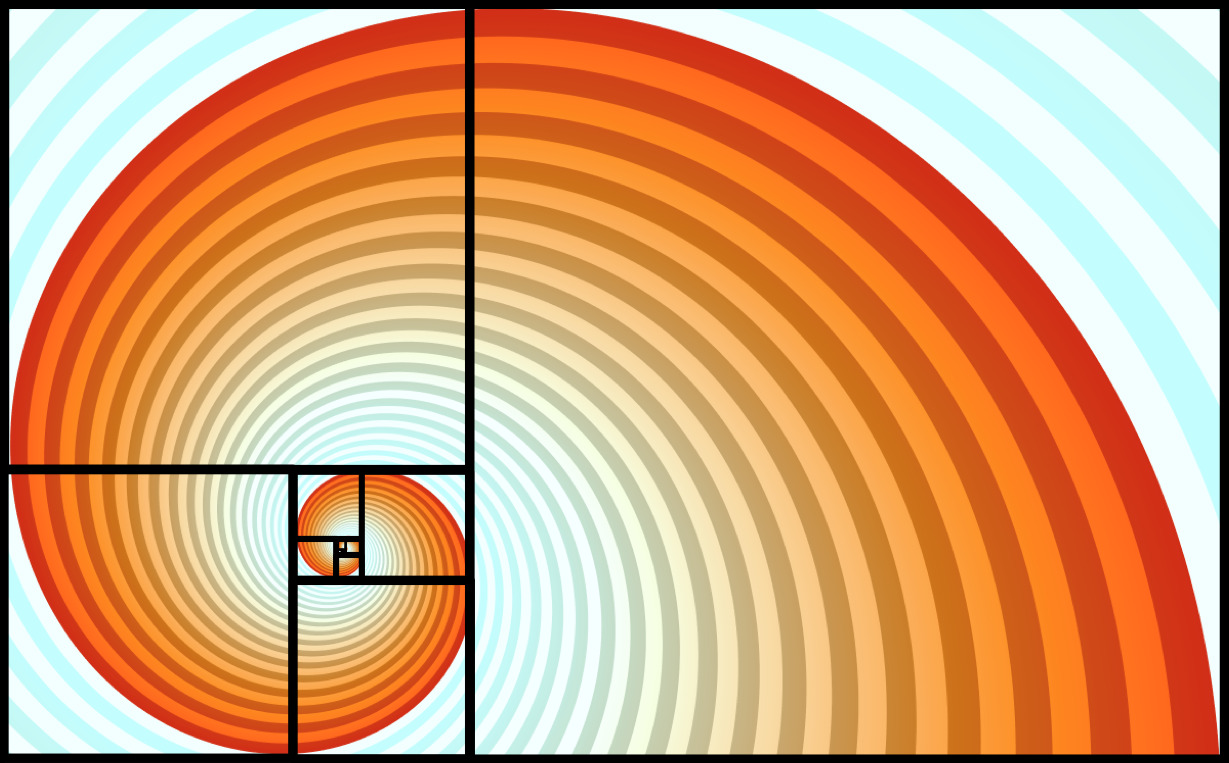
When a golden rectangle is recursively divided into further squares
and rectangles, and rotated curves are drawn in each square, a
pleasant logarithmic spiral is created. Similarly, a spiral
could be seeded with a small rectangle and grown outwards by adding
larger squares to it. Various spirals related to this can be found in
nature, such as the classic chambered nautilus shell, or the spiraling
seeds of sunflowers.
Fibonacci ratios
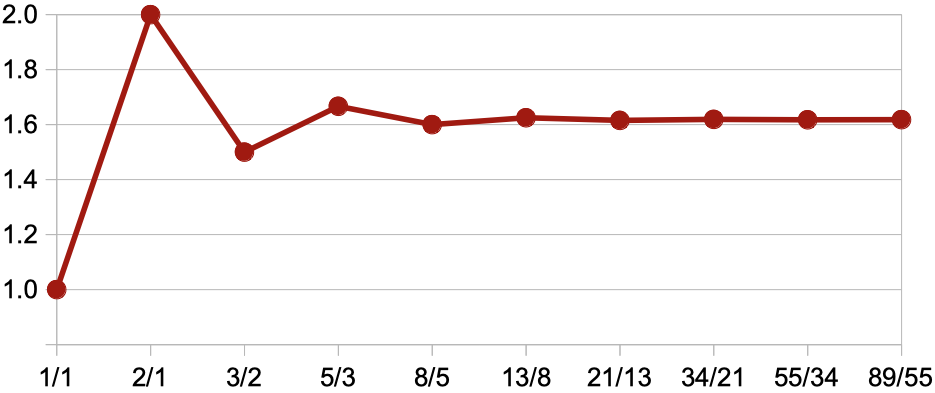
The growth rate of the Fibonacci numbers is φ. To generate the
Fibonacci sequence, start with 1, 1, and then repeatedly add the
previous two numbers in the sequence to generate the next number: 1,
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377... The ratio of a new
Fibonacci number to the previous one quickly converges to φ.
1 / 1 = 1.00000
2 / 1 = 2.00000
3 / 2 = 1.50000
5 / 3 = 1.66667
8 / 5 = 1.60000
13 / 8 = 1.62500
21 / 13 = 1.61538
34 / 21 = 1.61905
55 / 34 = 1.61765
89 / 55 = 1.61818
144 / 89 = 1.61798
233 / 144 = 1.61806
377 / 233 = 1.61803
The nth Fibonacci number can be calculated directly using:
round(φn / √5)
A logarithmic spiral like the one above can also be created from
squares with sizes relative to the Fibonacci numbers. In this case
the inner-most rectangle is composed of two squares instead of a
golden rectangle, which correspond to the two initial Fibonacci
numbers 1 and 1. But if these initial squares are small enough, the
spiral will look the same because the ratios of square sizes approach
φ as it grows.
Powers of φ
Like the Fibonacci numbers, any power of φ equals the sum of the
two previous powers of φ. This follows from φ2 =
φ + 1. If the Fibonacci sequence were seeded with 1,φ
instead of 1,1 the results would be the powers of φ.
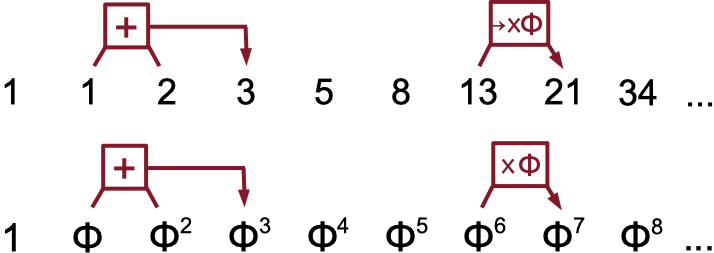
Any integer power of φ can be reduced to a factor of φ
plus a constant. These coefficients and constants follow the Fibonacci
sequence with the constants shifted by one. The positive powers can
be found by summing the two previous powers as described above:
φn = φn-1 + φn-2. The
negative powers can be found using φn =
φn+2 - φn+1 and follow a similar
pattern, but their coefficients and constants alternate signs.
φ1 = 1φ + 0
φ2 = 1φ + 1
φ3 = 2φ + 1
φ4 = 3φ + 2
φ5 = 5φ + 3
φ6 = 8φ + 5
φ7 = 13φ + 8
φ-1 = 1φ - 1
φ-2 = -1φ + 2
φ-3 = 2φ - 3
φ-4 = -3φ + 5
φ-5 = 5φ - 8
φ-6 = -8φ + 13
φ-7 = 13φ - 21
This shows the quirk that φn + φ-n is an
integer for even n, and φn - φ-n is
an integer for odd n, because the φ is canceled out. More
specifically, these give the sum of 2 Fibonacci numbers spaced 2
apart.
Convergent formulas
If any positive value of x is repeatedly updated with either of
these formulas, the new values converge to φ.
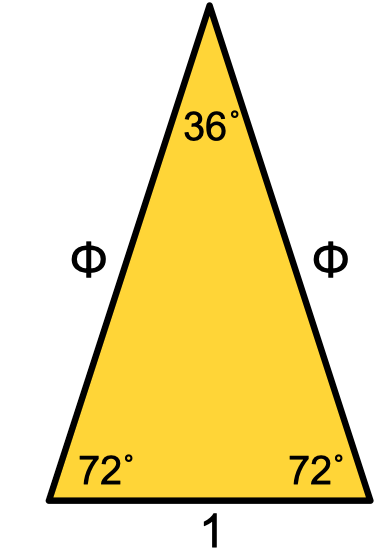
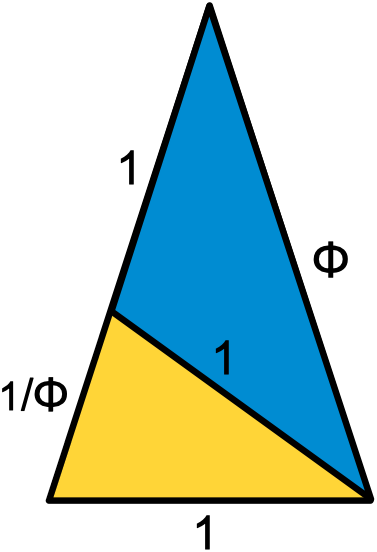
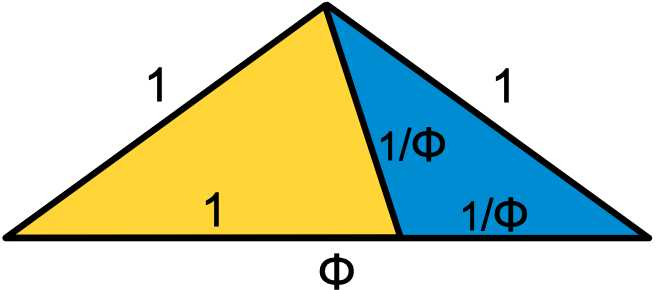
Golden triangles
Two isosceles triangles have sides with a φ ratio:
the acute golden triangle, and the obtuse golden gnomon.
 golden triangle
golden triangle
 golden gnomon
golden gnomon
Golden triangles and gnomons can be divided or combined to make new
golden triangles and gnomons. Their internal angles are all multiples
of 36° so they fit together nicely in multiple ways. This is
similar to how golden rectangles and squares are combined, but
with even more options. These also both show that 1/φ + 1 = φ.
Golden triangles and gnomons can be recursively divided in many ways,
to generate various geometric patterns, spirals, or fractals.

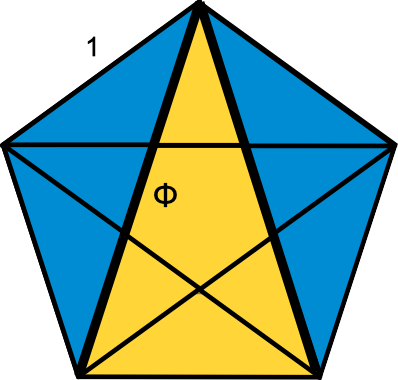
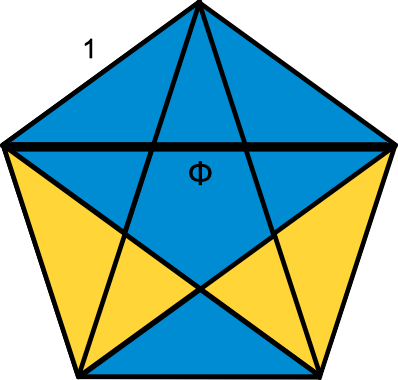
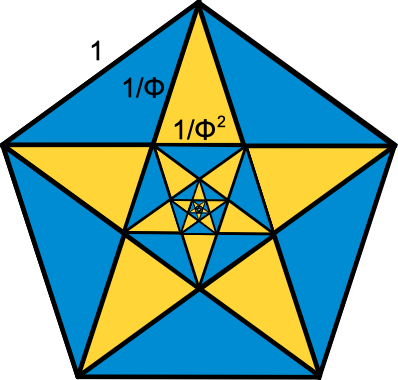
Pentagrams
Pentagrams contain many overlapping golden triangles and gnomons, so
their segment length ratios are related to φ. A regular pentagon
with sides of 1 has diagonals of length φ, the star within has
segments of 1/φ, and the inner pentagon has sides of
1/φ2. For pentagrams within pentagrams, the segment
lengths continue inwards in a reciprocal power-of-φ sequence.
Icosahedron vertices
If 3 golden rectangles are rotated to be mutually perpendicular in
3D as shown, their corners coincide with the 12 vertices of a regular
icosahedron. These points also align with the faces of a
dodecahedron. The dodecahedron is the dual of the icosahedron so
its face centers correspond to the icosahedron vertices.


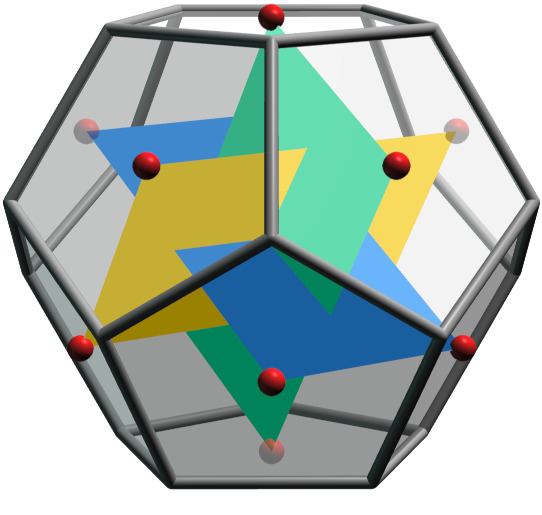
Icosahedron vertex coordinates can be found using:
[ ±φ, ±1, 0 ] for the yellow rectangle corners
[ 0, ±φ, ±1 ] for the green rectangle corners
[ ±1, 0, ±φ ] for the blue rectangle corners
Dodecahedron vertices
If 3 rectangles with a φ2 proportion (or 1/φ x
φ) are rotated to be mutually perpendicular in 3D, their 12
corners align with the vertices of a regular dodecahedron. The other
8 dodecahedron vertices align with the corners of a cube (not shown).
And these 20 points also align with the faces of an icosahedron.

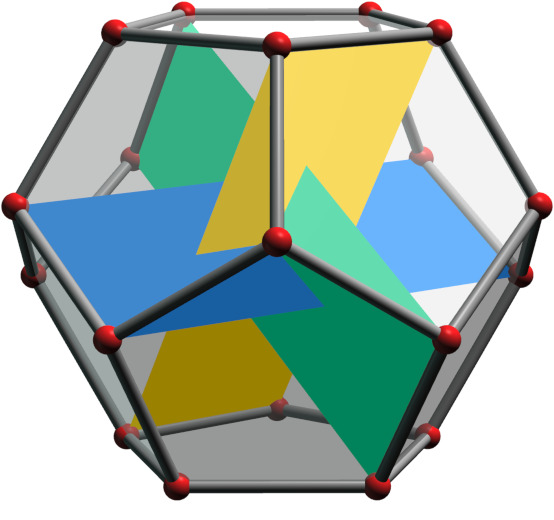

Dodecahedron vertex coordinates can be found using:
[ ±1/φ, ±φ, 0 ] for the yellow rectangle corners
[ 0, ±1/φ, ±φ ] for the green rectangle corners
[ ±φ, 0, ±1/φ ] for the blue rectangle corners
[ ±1, ±1, ±1 ] for the cube corners
References
For more information, visit the Wikipedia entries for the
golden ratio,
golden rectangle,
golden triangle,
Fibonacci sequence,
and
regular icosahedron.
© 2025, Karl Sims, All rights reserved.